實數完備性
今天金次終於用實數完備性證明了連續函數的中間值定理和極值定理(最大最小值定理),正式進入高等微積分。實數完備性的一個版本即「數列有上界遞增必收斂」,由此性質可導出絕妙的區間套定理:
此定理的直觀意義是,任意一個無窮縮小到消失的區間(以一個遞增數列 an 和一個遞減數列 bn 控制),最後會包到恰好一個實數。然後就是精彩的中間值定理證明:無窮的二分搜尋法!先列出連續函數的中間值定理:
證明時,就從 [a, b] 開始,用無窮的二分搜尋一步步縮小區間,期望借助區間套定理之力套住我們要的 c。演算法大概是這樣:取 [a, b] 中點,若這點的函數值為零,我們就找到所求的 c 了,結束。如果不為零,這點的函數值一定大於零或小於零,因此左半閉區間或右半閉區間兩者之一會符合「左端點之函數值和右端點之函數值異號」,就再對這個區間取中點,遞迴實施前述步驟。然而無窮的二分搜尋和一般的有窮二分搜尋有所差別,因為我們無法保證,無窮地縮小區間套最終能夠在某次取中點時找到 c,因此必須召喚出區間套定理保證無窮次嵌套後能夠套到唯一一個 c,而且 f(c) = 0。因為嵌套過程中,我們始終保持區間兩端的函數值異號,所以經無窮嵌套最後套到的那個實數之函數值會等於 0(中間一些論證細節省略)。
然後從區間套定理導出 Bolzano-Weierstrass 定理(這個有人會念嗎?XD),再用 B-W 定理導出一個 lemma,最後由另一個(等價的)實數完備性質「實數點集合若上方有界則有最小上界」聯合 B-W 定理和前述 lemma 之力證明了最大最小值定理(極值定理)。
極值定理的證明比較玄,目前還沒怎麼通透。區間套定理和中間值定理的證明大致理解,但論證上還是有一些 gap 沒撫平。金次發了第一次習題,總覺得應該不是現在能做,但又好像可以做 XD。高等微積分真是令人血脈賁張啊!
--
筆記幾乎來不及抄 XD。


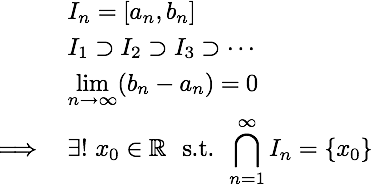
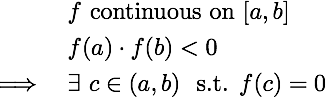
<< 回到主頁