Regular Languages
這是《Introduction to the Theory of Computation, 2/e》第一章 "Regular Languages" 重點融會整理 XD。
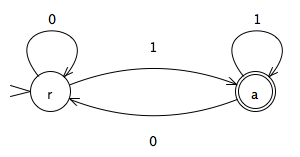
在探討計算理論的兩大主題 ─ computability、complexity ─ 之前,我們必須先對實施計算的機器 ─ 也就是計算機(computer) ─ 有所認識。Finite automata(有限自動機)就是一種(能力受限的)計算機。在此,計算的定義是將一個字串輸入機器,完畢後機器回報「接受」(accept)或「拒絕」(reject),也就是判定這個輸入字串是否屬於「這部機器所認得(recognize)的語言(language)」。所有 finite automata 認得的語言就稱為正則語言(regular languages),相對地任何一個正則語言都能找到一部 finite automaton 能認得它。(A language is regular iff some finite automaton recognizes it.)例如,以下這部 finite automaton 認得的語言是「所有以 1 結尾的字串」:
這部自動機一開始處於 r 狀態,隨著字串輸入,自動機的狀態就循著箭頭在 r 和 a 之間流轉,字串輸入完畢時若停在 a 則代表接受此字串,否則代表拒絕此字串。注意:「認得」(recognizes)這個詞代表的是自動機能夠(正確地)判定輸入字串在不在某個語言內(而不是「接受」輸入字串稱為「認得」)。例如 non-regular languages 就不能用 finite automata 辨識。另外有一種會精神分裂(XD)的 nondeterministic finite automata(NFA),表面上計算能力比 DFA(deterministic finite automata)還強,但經證明兩者等價。NFA 在 proof by construction 時相當方便,in particular 可方便地證明本章中作用於 regular languages 的三種操作(union、concatenation、star)具封閉性(closed)。
接著是 regular expressions,是用來描述 regular languages 的表述式。例如上述那部自動機所認得的語言以 regular expression 表述就是(假設組成字串的 alphabet 僅含 0 和 1):
經證明,regular expressions 所能描述的語言就是 regular languages,證明方式是展示 regular expressions 和 finite automata 之間可以互相轉換(可造一部 finite automata 辨識某個 regular expression 描述的語言,也可用 regular expression 表述一部 finite automata 所辨識的語言)。
最後是 regular languages 所滿足的一個必要性質(但非充分),其內字串都可拆解為三部份,並將中間那一段重複任意次(包括 0 次),此定理慣稱 pumping lemma。因為這性質必要而非充分,因此只能用來證明一個 language 不為 regular(無之必不然)。(另外也可用 regular operations 具封閉性證明某種語言不為 regular。)
總之,本章的主角就是 regular languages、finite automata、regular expressions 三者:有一類語言稱為 regular languages,可用 finite automata(包括 DFA & NFA)加以辨識,可用 regular expressions 加以描述。相對地,regular languages 也可用 finite automata 和 regular expressions 加以定義。
--
再來是 context-free languages。


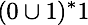
不錯,寫得真棒!
剛也看了其他幾篇文章,感覺你真是個認真的學生!呵!
<< 回到主頁